O princípio de Bernoulli afirma que para um fluxo sem viscosidade, um aumento na velocidade do fluido ocorre simultaneamente com uma diminuição na pressão ou uma diminuição na energia potencial do fluido. A equação foi nomeada como Bernoulli em homenagem ao matemático neerlandês-suiço Daniel Bernoulli que publicou o seu princípio, em seu livro Hydrodynamica em 1738.
Há basicamente duas formulações, uma para fluidos perfeitos e outra para fluidos reais.
- Equação Original
A forma original, que é para um fluxo incompressível sob um campo gravitacional uniforme (como o encontrado na Terra em pequenas altitudes), é:
ou
= velocidade do fluido ao longo do conduto
= aceleração da gravidade
= altura com relação a um referencial
= pressão ao longo do recipiente
= massa específica do fluido
As seguintes convenções precisam ser satisfeitas para que a equação se aplique:
- Escoamento sem viscosidade (“fricção” interna = 0)
- Escoamento em estado estacionário
- Escoamento incompressível (
constante em todo o escoamento)
- Geralmente, a equação vale a um conduto como um todo. Para fluxos de potencial de densidade constante, ela se aplica a todo o campo de fluxo.
A redução na pressão que ocorre simultaneamente com um aumento na velocidade, como previsível pela equação, é frequentemente chamado de princípio de Bernoulli.
A equação é dedicada a Daniel Bernoulli, embora tenha sido apresentada pela primeira vez da forma como está aí por Leonhard Euler.
- Equação para fluídos compreensíveis
Uma segunda forma mais geral da equação de Bernoulli pode ser escrita para fluidos compressíveis:
Aqui, 




A constante no lado direito da equação é frequentemente chamada de constante de Bernoulli e indicada pela letra “b”. Para o escoamento adiabático sem viscosidade e sem nenhuma fonte adicional de energia, “b” é constante ao longo de todo o escoamento. Mesmo nos casos em que “b” varia ao longo do conduto, a constante ainda prova-se bastante útil, porque está relacionada com a carga de pressãono fluido.
Quando uma onda de choque está presente, deve-se notar que um referencial move-se conjuntamente (comove-se) com uma onda de choque, muitos dos parâmetros envolvidos na equação de Bernoulli sofrem grandes modificações ao passar pela onda de choque. A constante de Bernoulli, porém, não se altera. A única exceção a essa regra são os choques radioativos, que violam as convenções que levam à equação de Bernoulli, como a falta de vazões ou fontes de energia.
- Dedução
Vamos começar com a equação de Bernoulli para fluidos incompressíveis.
A equação pode ser obtida pela integração das equações de Euler, ou pela aplicação da lei da conservação da energia em duas seções ao longo da corrente, e desprezando a viscosidade, a compressibilidade e os efeitos térmicos. Pode-se dizer que
- o trabalho mecânico feito pelas forças no fluido + redução na energia potencial = aumento na energia cinética.
O trabalho feito pelas forças é
A diminuição da energia potencial é
O aumento na energia cinética é
Juntando tudo, tem-se que
ou
Depois da divisão por 



ou 
A divisão adicional por g implica
Uma massa em queda livre de uma altura h (no vácuo), alcançará uma velocidade
ou
.
O termo 
A pressão hidrostática, carga estática ou altura estática é definida como
ou
.
O termo 
Uma maneira de ver como isto se relaciona com a conservação de energia diretamente é pela multiplicação pela densidade e volume unitário (que é permitido, já que ambos são constantes), resultando em:
e
A dedução para fluidos compressíveis é similar. Novamente, a dedução depende da (1) conservação da massa e (2) da conservação da energia.
A conservação da massa implica que no desenho acima, no intervalo de tempo 


.
Aplica-se a conservação da energia de uma maneira similar: assume-se que a mudança na energia do volume do duto limitado por 

onde 



A energia entrando por 

Uma expressão similar para 

Reescrevendo:
Agora, usando o resultado obtido anteriormente a partir da conservação da massa, isto pode ser simplificado de forma a se obter
que é a solução procurada.






 ou
ou 
 = velocidade do fluido ao longo do conduto
= velocidade do fluido ao longo do conduto = aceleração da gravidade
= aceleração da gravidade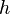 = altura com relação a um referencial
= altura com relação a um referencial = pressão ao longo do recipiente
= pressão ao longo do recipiente








 ou
ou  .
. ou
ou  .
. e
e
 .
.![Delta E_1 = left[ frac{1}{2} rho_1 v_1^2 + phi_1 rho_1 + epsilon_1 rho_1 + p_1 right] A_1 v_1 , Delta t](http://upload.wikimedia.org/wikipedia/pt/math/9/3/6/9364fdec271c653b66acf1071156bb5c.png)
![0 = left[ frac{1}{2} rho_1 v_1^2+ phi_1 rho_1 + epsilon_1 rho_1 + p_1 right] A_1 v_1 , Delta t - left[ frac{1}{2} rho_2 v_2^2 + phi_2rho_2 + epsilon_2 rho_2 + p_2 right] A_2 v_2 , Delta t](http://upload.wikimedia.org/wikipedia/pt/math/4/2/c/42ca460091570d3e1e4411e0f23f431c.png)
![0 = left[ frac{1}{2} v_1^2 + phi_1 + epsilon_1 + frac{p_1}{rho_1} right] rho_1 A_1 v_1 , Delta t - left[ frac{1}{2} v_2^2 + phi_2 + epsilon_2 + frac{p_2}{rho_2} right] rho_2 A_2 v_2 , Delta t](http://upload.wikimedia.org/wikipedia/pt/math/c/a/3/ca33bead05e8d1d09da0924e542c7923.png)




